Семинар 8. Оптимальное управление. Принцип максимума Понтрягина
Содержание
Материалы
Видеозаписи
Запись семинара: youtube (03.11.23)
Оптимальное управление
Постановка задачи
В вариационном исчислении мы рассматривали следующую задачу: \[ \int_0^T F(t,y,y') \, dt \rightarrow extr, \quad y(0) = y_0, \, y(T) = y_T \]
В оптимальном управлении возникает новое понятие - управление (обозначается как \(u(t)\)). Простой пример: машина движется по прямой, в начальный и конечный момент времени скорость равна нулю. Степень нажатия педали газа в такой задаче будет управлением (меняющимся от 0 до 1, где ноль это отпущенная педаль, а единица - педаль,нажатая "в пол").
Формально, задача оптимального управления может быть записана следующим образом: \[ \int_0^T F(t,y,u) \, dt \rightarrow \max \] \[ y' = f(t,y,u), \quad y(0) = y_0, \quad u \in U \]
Ремарка: далеко не всегда известно только начальное граничное условие. Может быть известно и конечное (но при этом может быть неизвестен конечный момент времени \(T\)).
В данной задаче важно следующее:
- \(y(t)\) непрерывен
- \(u(t)\) может иметь разрывы первого рода (устранимые, такие что пределы слева и справа существуют, но не равны друг другу)
Принцип максимума Понтрягина
Теорема. Для нахождения аналитического решения задачи оптимального управления можно использовать принцип максимума Понтрягина:
-
Выписываем гамильтониан: \[ H = F(t,y,u) + \lambda (t) f(t,y,u) \]
-
Находим максимум гамильтониана по управлению: \[ \max_{u \in U} H \] Важно отметить, что максимум может быть как внутренний, так и граничный
-
Решаем каноническую систему: \[ y' = \frac{\partial H}{\partial \lambda} \quad \land \quad \lambda' = - \frac{\partial H}{\partial y} \]
-
Для нахождения константы для уравнения для \(\lambda\) используем условие трансверсальности: \[ \left[ \lambda(t) \right]_{t=T} \Delta y_T + \left[ H \right]_{t=T} \Delta T = 0 \]
Замечание: для постановки задачи выше, где неизвестен \(y(T)\), условие превращается в \(\lambda(T) = 0\). Но в общем случае условие трансверсальности записано выше (оно пригодится на следующих семинарах).
Задача 1
Решите задачу оптимального управления: \[\int_0^2 y - u^2 \, dt \rightarrow \max, \quad y' = u, \quad y(0) = 0, \quad u \in \mathbb{R} \]
Решение
Идем по пунктам.
1. Гамильтониан
\[ H = y - u^2 + \lambda u \]
2. Максимум гамильтониана по управлению
Гамильтониан по управлению представляет собой параболу ветвями вниз. Управление может принимать любые значения, а значит существует только внутренний экстремум (вершина параболы): \[ H'_{u} = -2 u + \lambda = 0 \Rightarrow u = \lambda / 2 \]
3. Каноническая система
Сначала решаем уравнение для \(\lambda\): \[ \lambda' = - \frac{\partial H}{\partial y} = -1 \] \[ \lambda = -t + C_1 \]
Из условия трансверсальности (пункт 4) найдем константу: \[ \lambda(T) = 0 \Rightarrow -2 + C_1 = 0 \Rightarrow C_1 = 2 \] \[ \lambda(t) = -t + 2 \]
Отсюда мы получаем уравнение для управления (подставив уравнение для \(\lambda\)): \[u(t) = -\frac{t}{2} + 1\]
Переходим ко второму уравнению (для \(y\)): \[ y' = u = -\frac{t}{2} + 1\] \[ y = -\frac{t^2}{4} + t + C_2 \]
Из граничного условия найдем константу: \[ y(0) = 0 \Rightarrow C_2 = 0 \]
Ответ:
Траектория \[ y(t) = -\frac{t^2}{4} + t \] доставляет максимум функционалу при управлении \[u(t) = -\frac{t}{2} + 1\]
Задача 2
Решите задачу оптимального управления: \[\int_0^4 3y \, dt \rightarrow \max, \quad y' = y + u, \quad y(0) = 5, \quad u \in [0, 2] \]
Решение
Идем по пунктам.
1. Гамильтониан
\[ H = 3y + \lambda y + \lambda u \]
2. Максимум гамильтониана по управлению
Гамильтониан по управлению представляет собой линейную функцию. Управление может принимать значения от 0 до 2. В данной задаче максимум граничный и представляет собой следующий вид: \[ u = \begin{cases} 2, & \lambda > 0 \\ [0,2], & \lambda = 0 \\ 0, & \lambda < 0 \\ \end{cases}\] Несложно убедиться, что это действительно так. Лямбда может принимать любое значение. Если она больше нуля, то управление входит в гамильтониан со знаком плюс и мы берем максимально большое его значение (то есть 2). Если лямбда меньше нуля, то управление входит со знаком минус и берем наименьшее возможное значение управления (в данной задаче это 0). Если же лямбда равна 0, то гамильтониан не зависит от управления, а потому можем выбрать любое значение.
3. Каноническая система
Сначала решаем уравнение для \(\lambda\): \[ \lambda' = - \frac{\partial H}{\partial y} = -3 - \lambda \] \[ \lambda = C_1 e^{-t} - 3 \]
Из условия трансверсальности (пункт 4) найдем константу: \[ \lambda(T) = 0 \Rightarrow C_1 e^{-4} - 3 = 0 \Rightarrow C_1 = 3e^4 \] \[ \lambda(t) = 3e^{4-t} - 3 \]
Нарисуем график для \(\lambda(t)\):
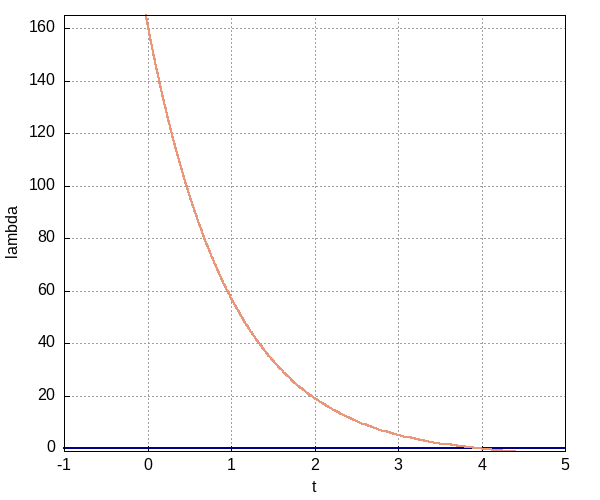
Видим, что на интервале \([0, 4)\) значение \(\lambda\) больше нуля, а значит \(u(t) = 2\). В точке \(t=4\) ситуация интересная, так как в данной задаче переключение управления попало на границу интервала. Формально правильно будет сказать, что здесь управление может быть любым, но и сказать, что управление равно двум тоже не будет ошибкой.
Переходим ко второму уравнению (для \(y\)): \[ y' = y + u = y + 2 \] \[ y = C_2 e^t - 2 \]
Из граничного условия найдем константу: \[ y(0) = 5 \Rightarrow C_2 - 2 = 5 \Rightarrow C_2 = 7 \]
Ответ:
Траектория \[ y(t) = 7e^t - 2 \] доставляет максимум функционалу при управлении \[u(t) = 2\]
Задача 3
Решите задачу оптимального управления: \[\int_{-1}^2 3y - 9u \, dt \rightarrow \max, \quad y' = y + 3u, \quad y(-1) = 0, \quad u \in [0, 1] \]
Решение
Идем по пунктам.
1. Гамильтониан
\[ H = 3y - 9u + \lambda y + \lambda 3 u = 3y + \lambda y + u (3\lambda - 9) \]
2. Максимум гамильтониана по управлению
Гамильтониан по управлению представляет собой линейную функцию. Управление может принимать значения от 0 до 1. В данной задаче максимум граничный и представляет собой следующий вид: \[ u = \begin{cases} 1, & 3\lambda - 9 > 0 \rightarrow \lambda > 3 \\ [0,1], & 3\lambda - 9 = 0 \rightarrow \lambda = 3 \\ 0, & 3\lambda - 9 < 0 \rightarrow \lambda < 3 \\ \end{cases}\]
3. Каноническая система
Сначала решаем уравнение для \(\lambda\): \[ \lambda' = - \frac{\partial H}{\partial y} = -3 - \lambda \] \[ \lambda = C_1 e^{-t} - 3 \]
Из условия трансверсальности (пункт 4) найдем константу: \[ \lambda(T) = 0 \Rightarrow C_1 e^{-2} - 3 = 0 \Rightarrow C_1 = 3e^2 \] \[ \lambda(t) = 3e^{2-t} - 3 \]
Нарисуем график для \(\lambda(t)\):
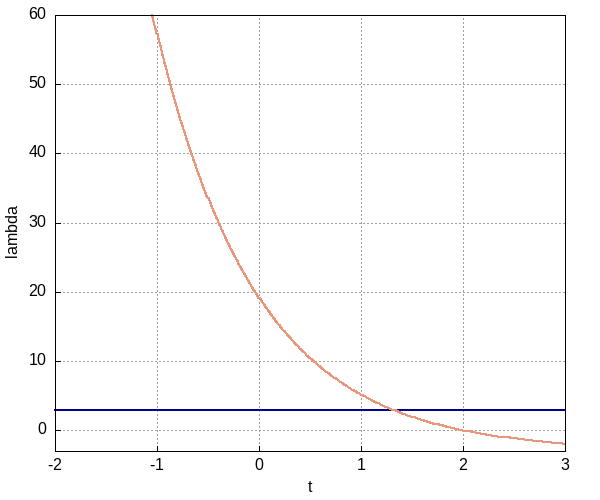
На графике видно, что на исследуемом интервале есть точка пересечения уравнения для \(\lambda(t)\) с \(\lambda = 3\). Можем найти ее: \[ 3e^{2 - \tau} - 3 = 3 \] \[ e^{2-\tau} = 2 \] \[\tau = 2 - \ln 2 \]
Слева от тау значение лямбда больше трех (а следовательно \(u = 1\)), а справа меньше трех (а, значит, \(u = 0\)). Поэтому решение будем искать на двух интервалах для \(t\).
Пусть \(t \in [-1, 2-\ln 2]\). Тогда имеем: \[ y' = y + 3 \] \[y = C_2 e^t - 3\]
Из граничного условия: \[ y(-1) = 0 \Rightarrow C_2 e^{-1} - 3 = 0 \Rightarrow C_2 = 3e \]
А решение имеет вид: \[ y(t) = 3e^{t+1} - 3 \]
Пусть \(t \in (2-\ln 2, 2]\). Тогда: \[y' = y\] \[ y = C_3 e^t \]
Для нахождения константы \(C_3\) воспользуемся тем, что \(y(t)\) должна быть непрерывна: \[ C_3 e^{2 - \ln 2} = 3e^{2 - \ln 2 + 1} - 3 \] \[ C_3 = \frac{3e^{3-\ln 2} - 3}{e^{2 - \ln 2}} \]
Ответ:
При \(t \in [-1, 2-\ln 2]\) траектория \[ y(t) = 3e^{t+1} - 3 \] доставляет максимум функционалу при управлении \[u(t) = 1 \]
При \(t \in (2-\ln 2, 2]\) траектория \[ y(t) = \frac{3e^{3-\ln 2} - 3}{e^{2 - \ln 2}} e^{t} \] доставляет максимум функционалу при управлении \[u(t) = 0 \]