Семинар 6. Достаточные условия экстремума. Простейшая портфельная задача
Содержание
Материалы
Видеозаписи
Запись семинара: youtube (15.10.23)
Достаточные условия экструмема
Условия Лежандра
Теорема. Функция \(y(t)\) является слабым минимумом (максимумом) вариационной задачи, если
- Функция \(y(t)\) - решение уравнение Эйлера и удовлетворяет граничным условиям
- \(y(t)\) может быть включена в поле экстремалей
- \(y(t)\) удовлетворяет усиленному условию Лежандра: \[ F_{y'y'} > 0 \quad (F_{y'y'} < 0) \] на кривой \(y(t)\).
Теорема. Функция \(y(t)\) является сильным минимумом (максимумом) вариационной задачи, если
- Функция \(y(t)\) - решение уравнение Эйлера и удовлетворяет граничным условиям
- \(y(t)\) может быть включена в поле экстремалей
- \(y(t)\) удовлетворяет условию Лежандра: \[ F_{y'y'} \geq 0 \quad (F_{y'y'} \leq 0) \] для любого \(y'\) и в некоторой окрестности \((t,y)\) рассматриваемой кривой.
Важное замечание: если не выполнен 2 и/или 3 пункт, то мы не можем утверждать, что полученное нами решение уравнения Эйлера не является экстремумом. Всё что мы можем сказать, это то, что с помощью теорем выше мы не можем ничего сказать о характере экстремума.
Задача 1
Исследовать функционал на экстремум \[ \int_0^2 ty' + y'^2 \, dt, \quad y(0) = 1, \, y(2) = 0 \]
Решение
Первый шаг. Используем уравнение Эйлера (первый специальный случай): \[ t + 2y' = C_1 \] \[ y' = C_2 - \frac{t}{2}, \quad C_2 = \frac{C_1}{2} \] \[ y = -\frac{t^2}{4} + C_2 t + C_3 \]
Из граничных условий получаем: \[ y(0) = 1 \Rightarrow C_3 = 1 \] \[ y(2) = 0 \Rightarrow -1 + 2 C_2 + 1 = 0 \Rightarrow C_2 = 0 \]
Исследуемая кривая имеет вид: \[ y(t) = -\frac{t^2}{4} + 1 \]
Второй шаг. Предъявим поле в области \(x \in [0, 2]\) в которое может быть включена наша траектория. Для этого "вернём" одну из констант, например на место, где была \(С_3\). Семейство кривых \(y = \frac{t^2}{4} + C\) образуют собственное поле (см. рисунок).
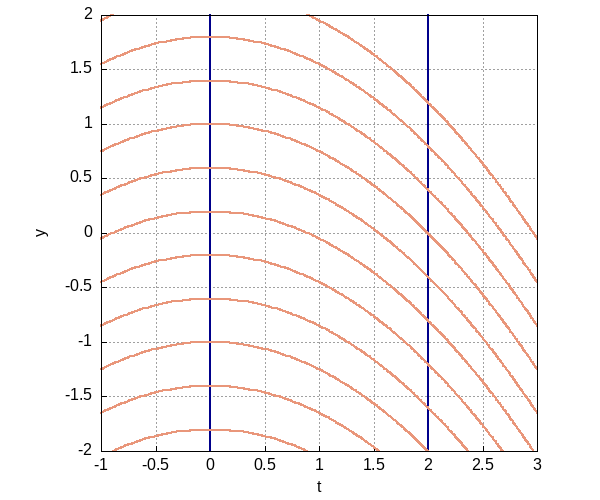
При \(C = 1\) исследуемая кривая включена в предъявленное поле экстремалей.
Третий шаг. Проверим условия Лежандра, найдя вторую частную производную интегранта по \(y'\): \[ F_{y'y'} = (t + 2y')'_{y'} = 2 \]
Получили константу большую нуля, а значит наша траектория это сильный (и слабый) минимум.
Ответ: \[ y(t) = -\frac{t^2}{4} + 1 \] - сильный минимум.
Задача 2
Исследовать функционал на экстремум \[ \int_0^1 \frac{1}{y'} \, dt, \quad y(0) = 0, \, y(1) = 1 \]
Решение
Первый шаг. Специальный случай \(F(y')\), а значит \[ y = C_1 t + C_2 \]
Из граничных условий получаем: \[y(t) = t\]
Второй шаг. Семейство кривых \(y = t + C\) образует собственное поле. При \(C = 0\) исследуемая функция включена в данное поле экстремалей.
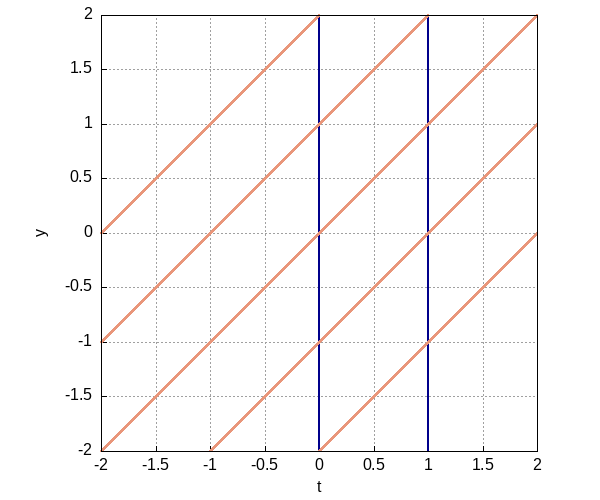
Третий шаг. Найдем вторую частную производную интегранта по \(y'\): \[ F_{y'y'} = \left( -\frac{1}{y'^2} \right)'_{y'} = \frac{2}{y'^3} \]
Проверим усиленное условие Лежандра: \[ y = t \Rightarrow y' = 1 \] Подставим в \(F_{y'y'}\): \[ \frac{2}{1^3} = 2 > 0 \] А значит исследуемая траектория является слабым минимумом.
Перейдем к проверке на сильный минимум/максимум. Требуется, чтобы \(F_{y'y'}\) сохранял знак для любого \(y'\). Приведем пример, что это не так: \[ y' = 1 \Rightarrow F_{y'y'} = 2 > 0 \] \[ y' = -1 \Rightarrow -2 < 0 \]
Получили, что условие Лежандра не выполнено, а значит это не сильный минимум/максимум.
Ответ: \(y(t) = t\) - слабый минимум.
Задача 3
Скоро будет. Пока можно посмотреть в записи семинара
Простейшая портфельная задача
Скоро будет. Пока можно посмотреть в записи семинара