Семинар 5. Условие трансверсальности. Задача Больцы. Собственное и центральное поле
Содержание
Материалы
Видеозаписи
Запись семинара: youtube (07.10.23)
Условие трансверсальности
По сути, дополнительное необходимое условие для задач с подвижным концом (либо неизвестно \(T\), либо \(y(T)\))
Теорема. Условие трансверсальности для задачи вариационного исчисления с функционалом вида \[ \int_{t_0}^{T} F(t, y(t), y'(t)) \, dt \] имеет вид \[ \left[ F - y'F_{y'} \right]_{t=T} \Delta T + \left[ F_{y'} \right]_{t=T} \Delta y_T = 0 \]
Задача 1
Найти допустимую экстремаль функционала \[ \int_0^{3\pi / 2} y'^2 + 4y \cos (t) - 8y \sin (t) \, dt, \quad y(0) = 1 \]
Решение
Используем уравнение Эйлера: \[ F_y = 4 \cos(t) - 8 \sin(t) \] \[ F_{y'} = 2 y' \] \[ y'' = 2\cos(t) - 4\sin(t) \] \[ y' = 2\sin(t) + 4 \cos(t) + C_1 \] \[ y = - 2 \cos(t) + 4 \sin(t) + C_1 t + C_2 \]
Из граничного условия имеем: \[ y(0) = 1 \Rightarrow -2 + C_2 = 1 \Rightarrow C_2 = 3 \]
Вторую константу находим, используя условие трансверсальности. \(T\) фиксирован (так как равен \(3\pi / 2\)), а значит \(\Delta T\) любое. \(y_T\) свободен (по условию неизвестно значение \(y(3\pi / 2)\)), а значит \(\Delta y_T\) любое. Чтобы было выполнено условие трансверсальности необходимо, чтобы: \[ \left[ F_{y'} \right]_{t=3\pi / 2} = 0 \] \[ 4\sin(t) + 8\cos(t) + 2 C_1 = 0 \left.\right|_{t = 3\pi / 2} \] \[ -4 + 2 C_1 = 0 \Rightarrow C_1 = 2 \]
Ответ: \[ y(t) = -2\cos(t) + 4\sin(t) + 2t + 3 \]
Задача 2
Найти допустимую экстремаль функционала \[ \int_0^T y'^2 + 2yy' - 16 y^2 \, dt, \quad y(0) = 0, \, y(T) = 0 \]
Решение
Используем уравнение Эйлера: \[ 2y' - 32y - \frac{d}{dt} (2y' + 2y) = 0 \] \[ 2y' - 32y - 2y'' - 2y' = 0 \] \[ y'' + 16y = 0 \] \[ \lambda^2 + 16 = 0 \Rightarrow \lambda = \pm 4i \] \[ y = C_1 \sin(4t) + C_2 \cos(4t) \]
Из ограничения для \(y(0)\) находим одну из констант: \[ y(0) = 0 \Rightarrow C_2 = 0 \] \[ y = C_1 \sin(4t), \, y' = 4 C_1 \cos(4t) \]
Для нахождения второй используем условие трансверсальности. В этой задаче не зафиксирован \(T\), а значит \(\Delta T\) любое. Следовательно, необходимо, чтобы: \[ \left[F - y'F_{y'} \right]_{t=T} = 0 \] \[ y'^2 + 2yy' - 16y^2 - y'(2y' + 2y) = 0 \] \[ y'^2 + 16y^2 = 0 \]
Вместо \(y\) и \(y'\) подставляем решение найденное выше (с учетом, что \(C_2 = 0\)): \[ 16C_1^2\cos^2(4t) + 16C_1^2\sin^2(4t) = 0 \] \[ C_1^2 (\cos^2 (4t) + \sin^2(4t)) = 0 \Rightarrow C_1 = 0 \]
Получили, что решение \(y(t) = 0\), но необходимо также определить значение для \(T\). Так как \(y(T) = 0\), то \(T\) - любое (так как для любого его значения \(y(T) = 0\) для нашего решения).
Задача Больцы
Устоявшееся название - задача Больца, но математика, её сформулировавшего, звали Оскар Больца. Поэтому, корректнее задача Больцы. К слову, поверхность Больцы (ссылка) называют правильно.
Лемма. Для задачи вариационного исчисления вида \[ \mathcal{B}(y(t)) = \int_{t_0}^{t_1} F(t, y(t), y'(t)) \, dt + G(y(t_0), y(t_1)) \rightarrow extr \] условие трансверсальности имеет вид: \[\begin{cases} \left[ F_{y'} \right]_{t=t_1} = & G_{y(t_1)} \\ \left[ F_{y'} \right]_{t=t_2} = - & G_{y(t_2)} \\ \end{cases}\]
Примечание: функцию \(G\) принято называть терминантом (напомню, что \(F\) называют интегрантом), а функционал \(\mathcal{B}\) - функционалом Больца/Больцы.
Задача 3
Найти допустимую экстремаль функционала \[ \int_1^2 t^2 y'^2 \, dt - 2 y(1) + y^2(2) \]
Решение
Решаем, используя уравнение Эйлера: \[ 0 - \frac{d}{dt}2 t^2 y' = 0 \] \[2t^2 y' = C_1\] \[ y' = \frac{C_2}{t^2}, \, C_2 = C_1 / 2 \] \[ y = - \frac{C_2}{t} + C_3 \]
Для нахождения констант используем условие трансверсальности для задачи Больцы: \[\begin{cases} 2 t^2 \frac{C_2}{t^2} = -2 \\ 2 t^2 \frac{C_2}{t^2} = -2 \left(-\frac{C_2}{2} + C_3 \right) \\ \end{cases}\] \[C_2 = -1, \, C_3 = \frac{1}{2} \]
Запишем ответ: \[ y(t) = \frac{1}{t} + \frac{1}{2} \]
Условия достаточности
Собственные и центральные поля
Определение. Семейство кривых образуют собственное поле в заданной области, если через каждую точку области проходит кривая, причем ровно одна.
Определение. Семейство кривых образуют центральное поле в заданной области, если через каждую точку области проходит кривая и все кривые пересекаются ровно в одной точке (её называют центром).
Задача 4
Образуют ли поле следующие семейства кривых в указанных областях:
- \(C e^x\) в области \(x^2 + y^2 \leq 1\)
- \((C + x)^2\) в области \(x^2 + y^2 \leq 1\)
- \(Cx\) в области \(x > 0\)
Решение
-
\(C e^x\) в области \(x^2 + y^2 \leq 1\)
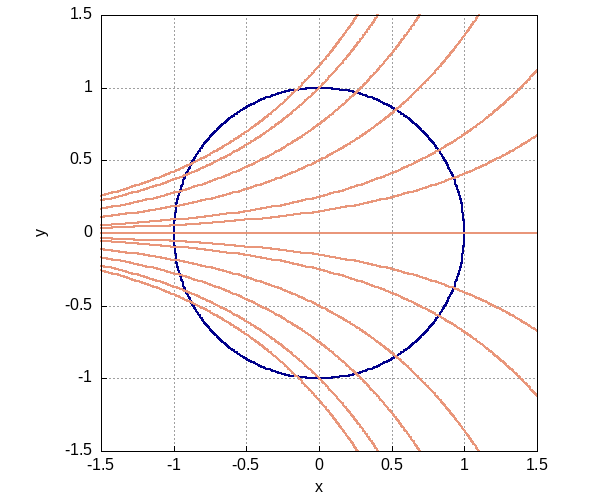
Figure 1: Кривые для разных значений C Собственное поле
-
\((C + x)^2\) в области \(x^2 + y^2 \leq 1\)
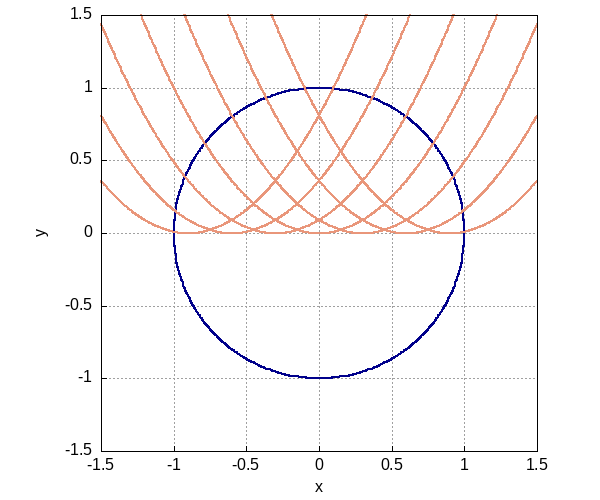
Figure 2: Кривые для разных значений C Не поле (не через каждую точку проходят и бесконечное число пересечений)
-
\(Cx\) в области \(x > 0\)
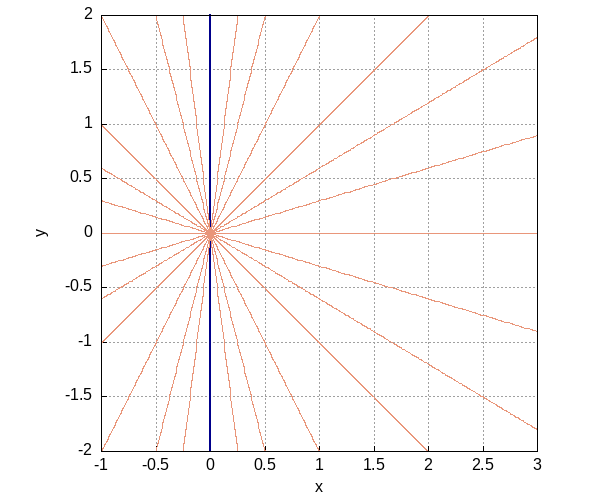
Figure 3: Кривые для разных значений C Собственное поле. Если в область добавим точку \((0,0)\), то центральное. Если \(x \geq 0\), то вообще не поле (так как ось y никогда не будет покрыта кривыми)