Семинар 3. Первая вариация функционала. Производная Гато
Содержание
Материалы
Видеозаписи
Запись семинара: youtube (23.09.23)
Вариация функционала
Классическая задача
Лагранж в 1760 году рассматривал классическую задачу: \[ J( x) = \int\limits _ { t _ {0} } ^ { {t _ 1 } } L( t, x ( t), \dot{x} ( t)) dt \]
Если для некоторой функции \(x_0(t)\) подставим \(x_0(t) + \alpha h(t)\), то получаем (в предположении непрерывности \(L\)): \[\tag{1} J( x _ {0} + \alpha h) = J( x _ {0} ) + \alpha J _ {1} ( x _ {0} )( h)+ r( \alpha ) \] где \(|r(\alpha)| \rightarrow 0\) при \(\alpha \rightarrow 0\), \(h(t)\) называют вариацией функции \(x_0(t)\) и обозначают \(\delta x_0(t)\).
Выражение \( J_1(x_0)(h) \), которое является функционалом по отношению к вариации \(h\), называют первой вариацией функционала и обозначают \(\delta J(x_0, h)\). В приложении к классической задаче (!) первая вариация имеет вид: \[ J_1(x_0)(h) = \int_{t_0}^{t_1} \left( L_{\dot{x}} \dot{h}(t) + L_{x} h(t) \right) dt \]
Для задач, отличных от постановки выше (например со слагаемым вне интеграла) можно использовать следующие способы:
-
Выделение линейной части приращения функционала.
Заменяем \(y \rightarrow y + \delta y, \, y' \rightarrow y' + \delta y'\). В выражении \( J(y + \delta y) - J(y) \) оставляем только слагаемые, линейные по вариации функции \(y\) и её производным, то есть \( \delta y, \, \delta y' \).
Замечание: \(\delta y \cdot \delta y'\) не подходит, по аналогии с тем, что \(x \cdot y\) это не линейная функция
-
Через частную производную по \(\alpha\):
\( \delta J = \frac{d}{d\alpha} J(y + \alpha \delta y) \left.\right|_{\alpha = 0} \). Эту формулу несложно получить из уравнения (1).
Производная по направлению
Определение. Производной по направлению для дифференцируемой в точке \(x_0\) функции \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) вдоль вектора (направления) \(v \in \mathbb{R}^n\) называют функцию: \[ \nabla_v f = \lim_{t \rightarrow 0} \frac{f(x_0 + tv) - f(x_0)}{t} \]
Обратим внимание, что для вычисления в направлении единичного вектора проще использовать: \[ \nabla_v f = \left\langle \nabla f, v \right\rangle \] где \(v\) в данном случае единичный вектор (орт). Ниже на изображении (взятом с Википедии) пример для функции \(f(x, y) = x^2 + y^2\) в точке \((-5, -5)\).
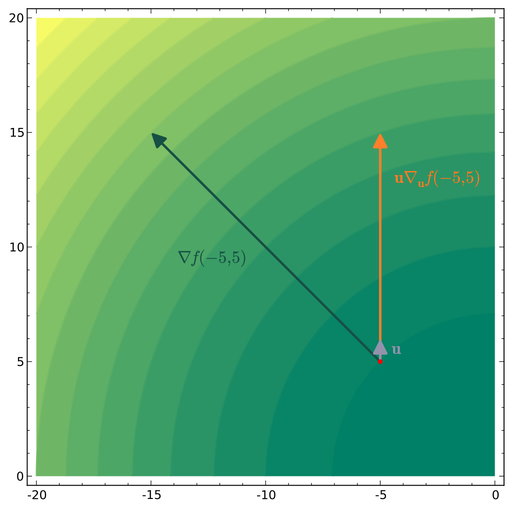
Производная Гато
В 1913 году Рене Гато предлагает обобщение первой вариации для бесконечномерного анализа. Пусть \(X, Y\) - линейные топологические пространства, тогда для отображения \(f: X \rightarrow Y\) вариация Гато (слабая вариация) задается следующим пределом (в топологии \(Y\)): \[ \delta f(x_0, h) = \frac{d}{dt} f(x_0 + th) \left. \right|_{t=0} = \lim_{t \rightarrow 0} \frac{f(x_0 + th) - f(x_0)}{t} \] в предположении, что он существует для всех \(h \in X\).
Начиная с работы Поля Леви 1922, принято предполагать линейность и непрерывность \(\delta f(x_0, h)\) по \(h\): \[ \delta f(x_0, h) = f'_G(x_0)h \] где (ограниченный) оператор \(f'_G: X \rightarrow Y\) называют производной Гато. \[ \ \]
Задачи на первую вариацию
Задача 1
\[J(y) = \int_a^b (y^2 - y'^2)dt\]
Найдите \(\delta J\)
Решение
Способ I. Выделение линейной части приращения функционала
\[ \Delta J = J(y + \delta y) - J(y) = \int_a^b \left( (y + \delta y)^2 - (y' + \delta y')^2 \right)dt - \int_a^b (y^2 - y'^2)dt = \] \[ = \int_a^b \left( y^2 + 2 y \delta y + (\delta y)^2 - y'^2 - 2 y' \delta y' - (\delta y')^2 \right) dt - \int_a^b (y^2 - y'^2)dt = \] \[ = \int_a^b \left( 2 y \delta y + (\delta y)^2 - 2 y' \delta y' - (\delta y')^2 \right) dt \]
В выражении под интегралом нам нужно оставить только те слагаемые, которые линейны по \( \delta y \) или \( \delta y'\): \[ \delta J = \int_a^b \left(2 y \delta y - 2 y' \delta y' \right)dt \] Это и есть ответ. Для краткости не буду дальше оборачивать подинтегральную функцию в скобки.
Способ II. Через производную по \(\alpha\)
\[ \delta J = \left. \frac{d}{d\alpha} \int_a^b (y + \alpha \delta y)^2 - (y' + \alpha \delta y')^2 dt \right|_{\alpha = 0} =\] \[ = \left. \int_a^b 2 (y + \alpha \delta y) \delta y - 2 (y' + \alpha \delta y') \delta y' \, dt \right|_{\alpha = 0} = \] \[ = \int_a^b 2 y \delta y - 2 y' \delta y' \, dt \]
Убедились, что решение двумя способами совпадает.
Задача 2
\[ J(y) = \int_{-1}^1 y'^2 + 2 y^3 y' + y \sin(t) \, dt \]
Найдите \(\delta J\)
Решение
Способ I. Выделение линейной части приращения функционала
\[\Delta J = \int_{-1}^{1} (y' + \delta y')^2 + 2 (y + \delta y)^3 (y' + \delta y') + (y + \delta y) \sin (t) \, dt - J(y) \] Обратим внимание, что нам от куба могут понадобиться гипотетически только \(y^3\) и \(3 y^2 \delta y\), так как дальше вариация функции будет во второй (\(3y \delta y^2\)) и третьей степени (\(\delta y^3\)). Перемножим их на скобку (\(y' + \delta y'\)) и отберем только линейные по вариации слагаемые: \(2 y^3 \delta y'\) и \(6 y^2 y' \delta y \) (не забываем про 2 перед произведением).
Аналогично из квадрата отбираем только \(2 y' \delta y'\) и пишем ответ:
\[ \delta J = \int_{-1}^{1} 2 y' \delta y' + 2 y^3 \delta y' + 6 y^2 y' \delta y' + \delta y \sin(t) \, dt \]
Способ II. Через производную по \(\alpha\)
\[ \delta J = \left. \frac{d}{d\alpha} \int_{-1}^{1} (y' + \alpha \delta y')^2 + 2 (y + \alpha \delta y)^3 (y' + \alpha \delta y') + (y + \alpha \delta y) \sin (t) \, dt \right|_{\alpha = 0} = \] \[ = \left. \int_{-1}^{1} 2(y' + \alpha \delta y')\delta y' + 6 (y + \alpha \delta y)^2 \delta y (y' + \alpha \delta y') + 2 (y + \alpha \delta y)^3 \delta y' + \delta y \sin (t) \, dt \right|_{\alpha = 0} = \] \[ = \int_{-1}^{1} 2 y' \delta y' + 6 y^2 y' \delta y + 2 y^3 \delta y' + \delta y \sin (t) \, dt \]
Задача 3
\[ J(y) = y^2(0) + \int_0^1 ty + y'^2 \, dt \]
Ответ
Единственная сложность в данной задаче, это понять, что \(y(0)\) здесь тоже надо воспринимать как функцию (с соответствующей вариацией). Ответ же: \[ \delta J = 2 y(0) \delta y(0) + \int_0^1 t \delta y + 2 y' \delta y' \, dt \]