← Назад

Семинар 1. Дифференциальные уравнения.

Содержание

• Материалы
  • Видеозаписи
  • Дополнительная литература
    • Базовая
    • Сложнее
• Введение
  • Физический пример
  • Виды дифференциальных уравнений
    • Обыкновенные дифференциальные уравнения (ordinary differential equations)
    • Уравнения в частных производных (partial differential equations)
  • Области применения дифференциальных уравнений
• Решение дифференциальных уравнений
  • Самое простое: \(y' = f(x)\)
    • Задача 1
  • Разделяющиеся переменные (separable equations)
    • Задача 2
  • Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами
    • Шаг 1. Однородное уравнение
    • Шаг 2. Неоднородная часть
    • Задача 3
    • Задача 4
    • Задача 5
    • Задача 6
    • Задача 7
• Геометрический смысл
  • Интегральные кривые поля направлений
    • Пример 1
    • Пример 2
  • Дифференциальное уравнение и его решение
• Дополнительные задачи
  • Задача 8
  • Задача 9*
  • Задача 10
  • Задача 11
  • Задача 12

Материалы

Видеозаписи

Запись семинара: youtube (09.09.23)

Лекция 0 (Дифференциальные уравнения - отдельные главы): youtube

Дополнительная литература

Базовая

• Романко В.К. Курс дифференциальных уравнений и вариационного исчисления (и сборник задач к нему)
• Tenenbaum M., Pollard H. Ordinary Differential Equations

Сложнее

• Арнольд В.И. Обыкновенные дифференциальные уравнения
• Hirsch M., Smale S., Devaney, R. Differential Equations, Dynamical Systems and an Introduction to Chaos

Введение

Физический пример

Вспомним второй закон Ньютона: \[F = ma \] где \(a\) - ускорение тела с массой \(m\), на которое действует сила \(F\).

Рассмотрим задачу свободного падения тела массы \(m\). Единственная действующая на него сила это \(mg\), где \(g\) - ускорение свободного падения.

Можем обозначить положение тела над фиксированной высотой как \(y\). Тогда скорость \(v\) есть ничто иное, как первая производная по времени: \[v = \frac{dy}{dt}\] а ускорение \(a\) - вторая производная: \[a = \frac{d^2y}{dt^2}\]

Используя второй закон Ньютона, получаем следующее дифференциальное уравнение: \[m \cdot \frac{d^2y}{dt^2} = m \cdot g \Rightarrow \frac{d^2y}{dt^2} = g \]

Можем немного усложнить задачу, добавив сопротивление воздуха, пропорциональное скорости тела, что отразится в силе, действующей на тело: \[m \cdot \frac{d^2y}{dt^2} = m \cdot g - k \cdot \frac{dy}{dt}, \quad k \in \mathbb{R}_{+} \]

Виды дифференциальных уравнений

Обыкновенные дифференциальные уравнения (ordinary differential equations)

Независимая переменная (обычно \(t\) или \(x\)) только одна, а дифференциальное уравнение для функции одной переменной. Порядок дифференциального уравнения это порядок наивысшей степени производной в нем.

• Модель Солоу-Свона (первого порядка)

  \[\frac{dk}{dt} = sf(k) - \delta k\]

• Уравнение Бесселя (второго порядка)

  \[x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2)y = 0\]

Уравнения в частных производных (partial differential equations)

Независимых переменных больше чем одна. Инструментарий для решения существенно отличается от обыкновенных дифференциальных уравнений (а также сильно сложнее), но в рамках курса они нам и не потребуются. Приведем несколько примеров (для расширения кругозора).

Пусть \(w = f(x,y,z,t)\) - функция от времени и координат точки в трехмерном пространстве. Существуют следующие уравнения в частных производных.

• Уравнение Лапласа

  \[\frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2} = 0\]

  Используется в механике, гидравлике, электростатике. Может быть задано для двухмерного и одномерного пространства.

• Уравнение теплопроводности

  \[a^2 \left( \frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2} \right) = \frac{\partial w}{\partial t}\]

  Описывает распределение температуры в заданной области пространства и ее изменение во времени. \(a\) - коэффициент температуропроводности, а \(w\) - температура в точке \((x, y ,z)\).

• Волновое уравнение

  \[a^2 \left( \frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2} \right) = \frac{\partial^2 w}{\partial t^2}\]

  Описывает волны или стоячие волны, как механические (звуковые, сейсмические), так и электромагнитные (включая световые). \(w\) - displacement from rest situation (отклонение от состояния покоя).

Области применения дифференциальных уравнений

Дифференциальные уравнения позволяют изучать всевозможные эволюционные процессы, обладающие следующими свойствами:

1. Детерминированность. Процесс называется детерминированным, если весь его будущий ход и все его прошлое определяется состоянием в настоящее время. Пример: в классической механике изучается движение систем, где будущее и прошлое однозначно определяется начальными положениями и скоростями всех точек системы.

2. Конечномерность. Процесс называется конечномерным, если его фазовое пространство конечномерно, то есть число параметров, нужных для его описания, конечно. Пример: в классической механике фазовое пространство системы из n точек имеет размерность 6n (по три координаты и по три компоненты скорости для каждой материальной точки)

3. Дифференцируемость. Процесс называется дифференцируемым, если его фазовое пространство имеет структуру дифференцируемого многообразия, а изменение состояния во времени описывается дифференцируемыми функциями.

Примерами таких процессов являются:

• процесс радиоактивного распада (состояние определяется количеством вещества) \[\frac{dN}{dt} = -\lambda N\] где \(\lambda \) - вероятность распада ядра в единицу времени.

• процесс размножения бактерий при фиксированном достаточном количестве питательного вещества (состояние определяется количеством бактерий) \[ \frac{dR}{dt} = kR \] где \(k > 0\) - коэффициент, который зависит от вида бактерий и условий среды.

Важное замечание: в естественных науках факт того, что процесс является детерминированным, конечномерным и дифференцируемым устанавливается экспериментально (и зачастую, является достаточно серьезным упрощением реальности), а потому устанавливается только с некоторой точностью.

Решение дифференциальных уравнений

Самое простое: \(y' = f(x)\)

Самый простой случай: \[\frac{dy}{dx} = f(x) \Rightarrow y = \int f(x) dx\]

Случай простой, но важно отметить, что неопределенный интеграл выше далеко не всегда может быть найден в терминах конечного числа элементарных функций. Примеры таких \(f(x)\): \[e^{-x^2}, \quad \frac{\sin x}{x}\]

Задача 1

\(y' = t^3 + 2\)

Решение

\(y = \frac{t^4}{4} + 2t + C, \, C \in \mathbb{R}\)

Разделяющиеся переменные (separable equations)

Дифференциальные уравнения следующего вида: \[\frac{dy}{dx} = f(x)g(y) \Rightarrow \frac{dy}{g(y)} = f(x)dx \Rightarrow \int \frac{dy}{g(y)} = \int f(x)dx \]

Задача 2

\(y' = 2xy\)

Решение

\(\frac{dy}{y} = 2x dx \Rightarrow \ln y = x^2 + C \Rightarrow y = \hat{C} e^{x^2}\)

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами

Дифференциальные уравнения следующего вида: \[ y^{(n)} + A_1 y^{(n-1)} + \ldots + A_{n-1} y' + A_n y = f(x) \]

Решение осуществляется в два шага:

1. Решение однородного уравнения (вместо \(f(x)\) ставим ноль в уравнении выше). Находим \(y_g\)
2. Нахождения решения для неоднородной части. Находим \(y_p\)

Теорема. Решение неоднородного дифференциального уравнения с постоянными коэффициентами имеет вид: \[y = y_g + y_p\]

Шаг 1. Однородное уравнение

Линейному однородному дифференциальному уравнению с постоянными коэффициентами можем сопоставить следующее характеристическое уравнение: \[\lambda^n + A_1 \lambda^{n-1} + \ldots + A_{n-1} \lambda + A_n \lambda^0 = 0\]

Теорема (решение однородного ду). Для корней характеристического уравнения верно следующее

1. Если \(\lambda \in \mathbb{R}\) - действительный корень кратности \(k\), то ему соответствуют решения \[e^{\lambda x}, \, x e^{\lambda x}, \, x^2 e^{\lambda x}, \ldots , \, x^{k-1} e^{\lambda x}\]
2. Если \(\lambda = \alpha \pm \beta i \in \mathbb{C}\) - комплексный корень кратности \(k\), то ему соответствуют решения \[e^{\alpha x} \sin \beta x, \, x e^{\alpha x} \sin \beta x, \ldots, \, x^{k-1} e^{\alpha x} \sin \beta x \] \[e^{\alpha x} \cos \beta x, \, x e^{\alpha x} \cos \beta x, \ldots, \, x^{k-1} e^{\alpha x} \cos \beta x \] Напоминание: комплексные корни всегда идут парами, так как если \(\lambda = \alpha + \beta i\) - корень, то и его комплексно сопряженное \(\alpha - \beta i\) тоже.

Шаг 2. Неоднородная часть

В рамках курса нам понадобятся \(f(x)\) только двух видов.

Теорема. Если \(f(x) = P_m(x)e^{\lambda x}\), то \(y_p\) имеет вид \[y_p = Q_m(x) e^{\lambda x} x^k\] где \(P_m, Q_m\) - полиномы степени \(m\), а \(k\) - кратность \(\lambda\) среди корней характеристического уравнения.

Теорема. Если \(f(x) = (P_m(x) \cos \beta x + Q_n(x) \sin \beta x) e^{\alpha x}\), то \(y_p\) имеет вид \[y_p = (S_m(x) \cos \beta x + R_n(x) \sin \beta x) e^{\alpha x} x^k\] где \(P_m, S_m, Q_n, R_n\) - полиномы степеней \(m\) и \(n\) соответственно, а \(k\) - кратность \(\alpha \pm \beta i\) среди корней характеристического уравнения.

Задача 3

\(y''' - y' = 0\)

Решение

Выпишем характеристическое уравнение и найдем его корни \[\lambda^3 - \lambda = 0\] \[\lambda (\lambda^2 - 1) = 0\] \[\lambda_1 = 0, \, \lambda_{2,3} = \pm 1\]

Получаем соответствующее решение дифференциального уравнения \[y(x) = C_1 e^{0 \cdot x} + C_2 e^{1 \cdot x} + C_3 e^{-1 \cdot x} = C_0 + C_1 e^{x} + C_2 e^{-x}\]

Задача 4

\(y''' - 3 y'' + 3 y' - y = 0\)

Решение

Выпишем характеристическое уравнение и найдем его корни. В данной задаче требуется увидеть формулу куба разности \[\lambda^3 - 3 \lambda^2 + 3 \lambda - 1 = 0 \] \[(\lambda - 1)^3 = 0\] \[\lambda_{1,2,3} = 1\]

Получили корень кратности 3. Запишем решение: \[y(x) =C_1 e^{x} + C_2 x e^{x} + C_3 x^2 e^{x} = (C_1 + C_2 x + C_3 x^2 ) e^x \]

Задача 5

\(y'' + a^2 y = 0\), где \(a > 0\)

Решение

Выпишем характеристическое уравнение и найдем его корни \[\lambda^2 + a^2 = 0\] \[\lambda = 0 \pm ai\]

В данной задаче получили комплексный некратный корень. Пишем ответ \[y(x) = C_1 \cos ax + C_2 \sin ax\]

Задача 6

\(y'' + y = x^2 + x\)

Решение

Выпишем характеристическое уравнение для однородного дифференциального уравнения и найдем его корни \[\lambda^2 + 1 = 0\] \[\lambda_{1,2} = \pm i\]

Выпишем решение однородного уравнения \[y_g = C_1 \sin x + C_2 \cos x\]

Переходим к неоднородной части. \(\lambda = 0\) не является корнем характеристического многочлена, а потому решение будем искать в виде \[y_p = Ax^2 + bx + c\] так как \(f(x)\) в нашей задаче является полиномом второй степени. Для подстановки в исходное уравнение, необходимо найти \(y_p''\) \[y_p' = 2Ax + b\] \[y_p'' = 2A\]

Подставляем частные решения в исходные уравнения, чтобы определить коэффициенты \[2A + Ax^2 + bx + c = x^2 + x\] Приравнивая левую и правую часть при \(x\) одной степени, получаем \[A = 1\] \[b = 1\] \[2A + c = 0 \Rightarrow 2 + c = 0 \Rightarrow c = -2\]

Запишем ответ \[y(x) = C_1 \sin x + C_2 \cos x + x^2 + x - 2\]

Задача 7

\(y'' - y' = x - 2\)

Решение

Выпишем характеристическое уравнение для однородного дифференциального уравнения и найдем его корни \[\lambda^2 - \lambda = 0\] \[\lambda_1 = 0, \lambda_2 = 1\] \[y_g = C_1 + C_2 e^x\]

В данном примере \(\lambda = 0\) из неоднородной части является корнем характеристического многочлена, а потому частное решение будем искать вида \[y_p = (bx +c) \cdot x\] \[y_p' = 2bx + c \] \[y_p'' = 2b\]

Найдем коэффициенты частного решения \[2b - 2bx - c = x - 2\] \[-2b = 1 \Rightarrow b = -1/2\] \[2b - c = -2 \Rightarrow c = 1\]

Запишем ответ \[y(x) = C_1 + C_2 e^x - \frac{x^2}{2} + x\]

Геометрический смысл

Интегральные кривые поля направлений

Определение. Предположим, что в каждой точке некоторой области на плоскости выбрана проходящая через эту точку прямая. Будем говорить, что в этом случае в этой области задано поле направлений.

Замечания:

• две гладкие кривые, проходящие через одну точку, задают одно направление только если они касаются. Поэтому прямые в определении выше можно заменить произвольными гладкими кривыми (важна лишь касательная)
• для n-мерного пространства поле направлений определяется аналогичным образом

Определение. Линия, которая в каждой своей точке касается имеющегося в этой точке направления поля, называется интегральной кривой поля.

Теорема. Задача отыскания интегральных кривых такого поля есть в точности задача интегрирования данной непрерывной функции.

В общем случае задача отыскания интегральных кривых не сводится к операции интегрирования: даже для очень просто задаваемых полей направлений на плоскости уравнения интегральных кривых нельзя представить конечными комбинациями элементарных функций и интегралов.

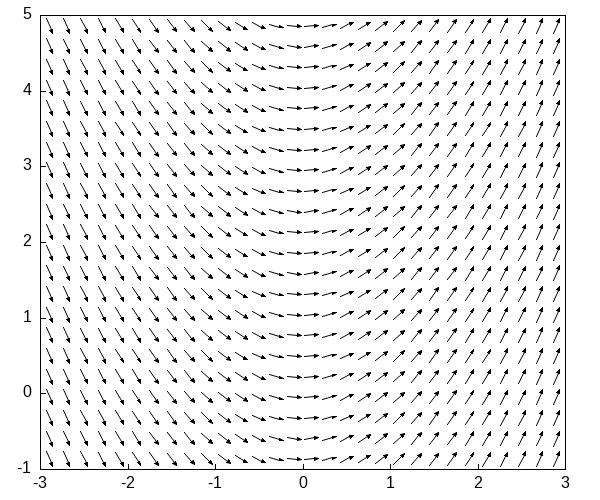
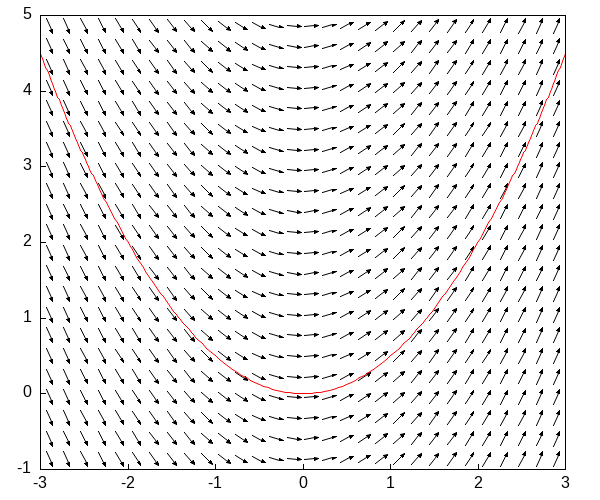
Пример 1

\(\dot{y} = t\)

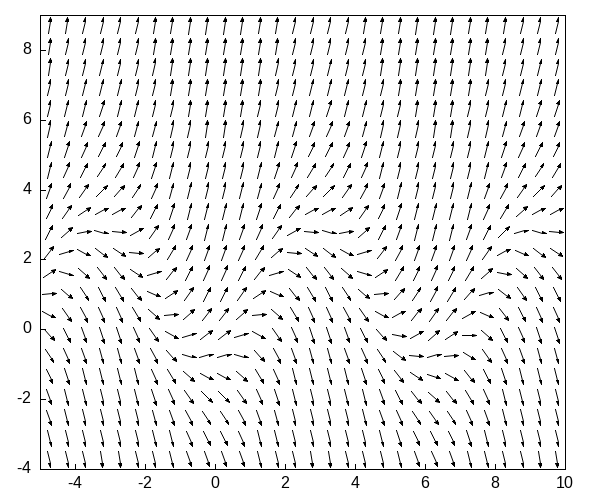
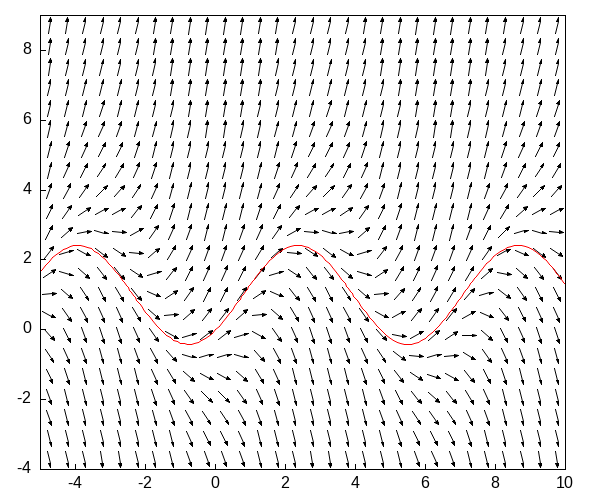
Пример 2

\(\dot{y} = 2\cos(t)-1+y\)

Дифференциальное уравнение и его решение

Геометрическая задача нахождения интегральных кривых аналитически может быть записана как задача нахождения решений дифференциального уравнения.

Пусть поле направлений на плоскости \((t, y)\) не содержит вертикальных направлений (параллельных оси ординат \(y\)). Тогда тангенс \(\nu(t, y)\) угла наклона приложенной в точке \((t, y)\) прямой поля направлений к оси абсцисс конечен и интегральные кривые являются графиками функции \(y = \varphi(t)\) (с областью определения \(I\) на \(t\)).

Теорема. Для того, чтобы график функции \(\varphi(t)\) был интегральной кривой, необходимо и достаточно, чтобы для всех \(t \in I\) было выполнено: \[ \frac{d\varphi}{dt} = \nu(t, \phi(t)) \]

Наконец, введем определение решения дифференциального уравнения:

Определение. Функция \(\varphi(t)\) называется решением дифференциального уравнения \[y' = \nu(t, y)\].

Примечание: производную по времени часто обозначают как \(\dot{y}\), а уравнение выше, соответственно: \[ \dot{y} = \nu(t, y) \]

Определение. Решение \(\varphi(t)\) удовлетворяет начальному условию \((t_0, y_0)\), если \(\varphi(t_0) = x_0\).

Дополнительные задачи

Задача 8

\(y' \sin y = x^2\)

Решение

Уравнение в разделяющихся переменных \[\sin y \,\, dy = x^2 dx\] \[-\cos y = \frac{x^3}{3} + C_1\] \[y(x) = \arccos \left(C_1 - \frac{x^3}{3} \right)\]

Задача 9*

\(y' \sin x = 1\)

Решение

Уравнение в разделяющихся переменных \[dy = \frac{dx}{\sin x}\]

Найдем интеграл косеканса \[\int \frac{dx}{2 \sin \frac{x}{2} \cos \frac{x}{2}} = \int \frac{d(\frac{x}{2})}{\tan \frac{x}{2} \cos^2 \frac{x}{2}} = \int \frac{d({\tan \frac{x}{2}})}{\tan \frac{x}{2}} = \ln \left| \tan \frac{x}{2} \right| + C_1 \]

Запишем ответ \[y(x) = \ln \left| \tan \frac{x}{2} \right| + C_1\]

Задача 10

\(y \log y \, dx - x \, dy = 0\)

Решение

Уравнение в разделяющихся переменных \[ \frac{dy}{y \log y} = \frac{dx}{x} \]

Интеграл слева возьмем по частям (\(\int u dv = uv - \int v du\)) \[ \frac{dy}{y \log y} = \left[ v = \frac{y^2}{2}, \, u = \log y , \, du = \frac{1}{y} dy \right] = \frac{y^2}{2} \log y - \int \frac{y^2}{2} \cdot \frac{1}{y} dy = \] \[\frac{y^2}{2} \log y - \frac{y^2}{4} + C = \frac{y^2}{4} \left( 2\log y - 1 \right) + C\]

Запишем ответ \[\frac{y^2}{4} \left( 2\log y - 1 \right) = \log x + C_1\]

Задача 11

\(y^{(4)} + 2 y'' + y =0\)

Решение

Выпишем характеристический многочлен и найдем корни. Обратим внимание, что это биквадратное уравнение \[\lambda^4 + 2 \lambda + 1 = 0\] \[(\lambda^2 + 1)^2 = 0\] \[\lambda_{1,2} = \pm i, \, \lambda_{3,4} = \pm i\]

Получили комплексный корень \(\pm i\) кратности 2. Пишем ответ \[y(x) = (C_1 + C_2 x) \cos x + (C_3 + C_4 x) \sin x\]

Задача 12

\(y^{(4)} + 2 y'' + y = \sin x\)

Решение

Однородное решение совпадает с предыдущей задачей. Неоднородная часть с \(0 \pm i\) кратности два, поэтому решение ищем вида \[y_p = x^2(A\sin x + B\cos x)\]

Коэффициенты находим аналогично предыдущим задачам (вычислив \(y_p''\) и \(y_p^{(4)}\))