Семинар 7. Избранные сюжеты лагранжевой механики
Содержание
Материалы
Видеозаписи
Запись семинара: youtube (21.10.23)
Энергия
Определение. Если тело или система тел способны совершить работу, то говорят, что они обладают энергией. То есть энергия это физическая величина, характеризующая способность тела совершать работу.
Обозначается буквой \(E\). Измеряется в джоулях (в тех же единицах, что и работа).
Определение. Потенциальной энергией называется энергия взаимодействия тел или частей одного тела.
Пример 1. Потенциальная энергия тела, поднятого над Землей
Для того, чтобы поднять тело на высоту \(h\) над "Землей" (точнее над некоторой фиксированной высотой) необходимо выполнить следующую работу: \[ A = F \cdot h = mgh \]
При подъеме тела была совершена работа, и теперь поднятое тело обладает равной данной работе потенциальной энергией, то есть: \[ E_p = V = mgh \]
Определение. Кинетической энергией называется энергия, которой обладает движущееся тело.
Вычисляется следующим образом: \[ E_k = T = \frac{mv^2}{2} \]
Отдельно отмечу, что здесь скорость это именно скаляр, а не вектор.
Утверждение. Если в системе отсутствуют силы трения, то уменьшение потенциальной энергии приводит к увеличению кинетической на равную величину. Кроме того, в такой системе сумма потенциальной и кинетической энергии (полная механическая энергия) постоянна.
Задача 1
В системе без сил трения нитяный маятник находится в состоянии покоя. Ему сообщается скорость равная 2 м/с. На какую максимальную высоту он поднимется?
Решение
В нижней точке: \[ V_1 = 0; \quad T_1 = \frac{mv^2}{2} \]
В верхней точке: \[ V_2 = mgh; \quad T_2 = 0 \]
Из закона сохранения имеем: \[ 0 + \frac{mv^2}{2} = mgh + 0 \] \[ h = \frac{v^2}{2g} \]
Подставив заданную скорость получаем ответ: \[ h = \frac{2}{g} \]
Принцип наименьшего действия
Рассмотрим следующую величину: \[ S (x(t)) \equiv \int_{t_1}^{t_2} L(x, \dot{x}, t) \, dt \] которая называется действием. Из выражения выше видно, что действие это скалярный функционал, зависящий от траектории тела (\(x(t)\)). Размерность действия это (Энергия)\(\times\)(Время).
Теорема. Если функция \(x_0(t)\) является стационарным значением (то есть локальный минимум, максимум или седловая точка) действия \(S\), то верно следующее выражение (уравнение Эйлера-Лагранжа) в предположении, что концы функции фиксированы (\(x(t_1) = x_1, \, x(t_2) = x_2\)): \[ \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{x}_0} \right) = \frac{\partial L}{\partial x_0} \]
Вспоминая лекции, можем отметить что уравнение Эйлера выводится из равенства нулю первой вариации: \[ \delta S = \int_{t_1}^{t_2} L(x + \alpha \delta x, \dot{x} + \alpha \delta \dot{x}, t) \, dt = \int_{t_1}^{t_2} L_{x} \delta x + L_{\dot{x}} \delta \dot{x} \, dt = 0 \] что является математическим выражением принципа наименьшего действия. Содержательно же имеем следующее.
Принцип наименьшего действия (другое название, принцип Гамильтона) состоит в том, что траектория частицы это такая траектория, которая доставляет действию стационарное значение. То есть уравнение Эйлера является эквивалентом второго закона Ньютона (\(F = ma\)).
Важное замечание: внимательный слушатель/читатель может задаться вопросом, а почему частицы вообще выбирают стационарные траектории. К сожалению, простого (да и, честно говоря, сложного тоже) ответа на этот вопрос нет. Но экспериментальные данные не противоречат нашим предположениям. Сюда же идет вопрос, почему Лагранжиан имеет ровно такой вид и работает в принципе.
Последнее важное замечание: выше шла речь об одномерных задачах, но если Лагранжиан \(L\) зависит от \(x_1(t), x_2(t), \ldots\), то ничего сверх принципа наименьшего действия нам не требуется (см. семинар про обобщения уравнения Эйлера).
Лагранжевая механика
Рассмотрим следующую физически бессмысленную комбинацию кинетической (\(T\)) и потенциальной (\(V\)) энергии: \[ L \equiv T - V \] Выражение \(L\) называется Лагранжианом (в выкладках выше речь шла как раз таки о нем). Не смотря на отсутствие физического смысла у Лагранжиана, он оказывается полезным. Более того, в многомерных задачах решение с помощью Лагранжиана оказывается существенно проще из-за того, что энергии это скаляры, а силы (которые нужны для \(F = ma\)) - вектора.
Рассмотрим задачу тела, закрепленного на конце пружины, находящегося на столе без трения (эту задачу мы рассматривали на первом семинаре, записывая решения с помощью второго закона Ньютона, перечисляя силы, действующие на тело). Кинетическая энергия рассчитывается стандартно по формуле: \[ T = \frac{mv^2}{2} = \frac{m\dot{x}^2}{2} \] Потенциальная энергия в данной задаче рассчитывается приближенно с помощью закона Гука (про упруго деформированные тела): \[ V = \frac{k x^2}{2} \] где \(k\) - жесткость деформированного тела.
Выпишем Лагранжиан и, затем, уравнение Эйлера-Лагранжа: \[ L = \frac{1}{2} m \dot{x}^2 - \frac{1}{2} k x^2 \] \[ -kx - \frac{d}{dt} (m \dot{x}) = 0 \] \[ m\ddot{x} + kx = 0 \]
Получили результат, совпадающий с тем, что было на первом семинаре (где выписывали через второй закон Ньютона). Еще немного терминологии: уравнение, которое мы выше вывели из уравнения Эйлера-Лагранжа называется уравнением движения. Термин несколько путанный, так как относится к дифференциальному уравнению второго порядка, а не к непосредственно к уравнению для траектории \(x(t)\), которое в данной задаче имеет вид: \[ x(t) = A \cos \left( \omega t + \varphi \right) \]
Важное замечание: метод выше начинает терять свою притязательность тогда, когда в задаче появляются неконсервативные силы, например силы трения. Всё ещё можно использовать, но их вручную придется добавлять в уравнение Эйлера-Лагранжа.
Задача 2
Рассмотрим движение частицы по параболической траектории (под действием гравитации) на плоскости. Найти уравнения для \(x(t)\) и \(y(t)\).
Решение
Выпишем кинетическую энергию: \[ T = \frac{1}{2} m\dot{x}^2 + \frac{1}{2} m \dot{y}^2 \]
Выпишем потенциальную энергию: \[ V = mgy \]
Теперь запишем Лагранжиан: \[ L = \frac{1}{2}m(\dot{x}^2 + \dot{y}^2) - mgy \]
Используя уравнение Эйлера-Лагранжа, найдем решение по \(x(t)\): \[ 0 - \frac{d}{dt} \left( \frac{1}{2} \cdot 2 m \dot{x} \right) = 0 \] \[ \ddot{x} = 0 \] \[x_t = v_{x_0} t\]
Аналогично для \(y(t)\): \[ -mg - m\ddot{y} = 0 \] \[ y = v_{y_0} t - \frac{1}{2}gt^2 \]
Задача 3
Дана следующая система грузов (движутся вертикально) и пружин:
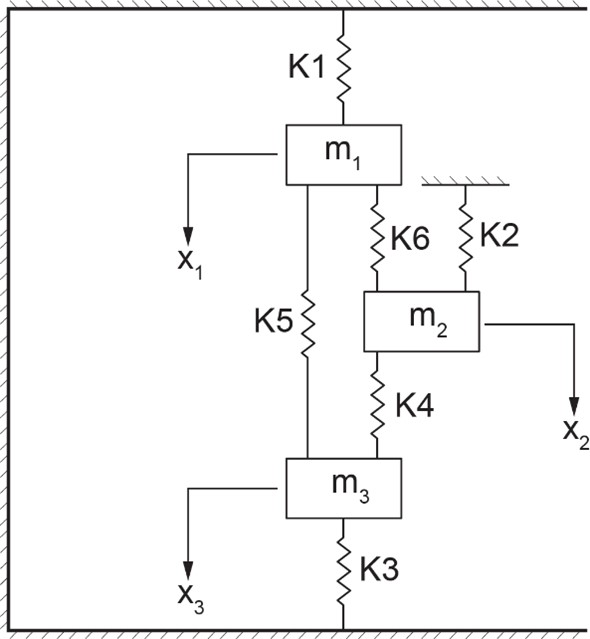
Решение
Выпишем кинетическую энергию: \[ T = \frac{1}{2} (m_1\dot{x}_1^2 + m_2 \dot{x}_2^2 + m_3 \dot{x}_3^2) \]
Выпишем потенциальную энергию (первое слагаемое для пружин, связывающих с фиксированными поверхностями, следующие - для пружин соединяющих тела между собой): \[ V = \frac{1}{2} (k_1 x_1^2 + k_2 x_2^2 + k_3 x_3^2) + \frac{1}{2} k_4 (x_2 - x_3)^2 + \frac{1}{2} k_5 (x_1 - x_3)^2 + \frac{1}{2} k_6 (x_1 - x_2)^2 \]
Применяя уравнение Эйлера к каждому телу масс (оно же степень свободы системы), получим систему обыкновенных дифференциальных уравнений: \[\begin{bmatrix} m_1 & 0 & 0 \\ 0 & m_2 & 0 \\ 0 & 0 & m_3 \\ \end{bmatrix} \begin{bmatrix} \ddot{x}_1 \\ \ddot{x}_2 \\ \ddot{x}_3 \\ \end{bmatrix} + \begin{bmatrix} k_1 + k_5 + k_6 & -k_6 & -k_5 \\ -k_6 & k_2 + k_4 + k_6 & -k_4 \\ -k_5 & -k_4 & k_3 + k_4 + k_5 \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \end{bmatrix}\]
Другие приложения вариационного исчисления
Далеко не все полезные применения вариационного исчисления ограничиваются разностью энергий. Далее рассмотрим две задачи:
- [Задача о брахистохроне] Задача \( T \rightarrow \min \) может быть сведена к задаче вариационного исчисления: \[ T \rightarrow \min \Leftrightarrow \int_0^T 1 \, dt \rightarrow \min \]
- [Задача Дидоны] Интеграл Римана имеет вполне конкретный физический смысл (площадь под кривой), что может быть также полезно
Задача о брахистохроне
Скоро будет. Пока можно посмотреть в записи семинара
Задача Дидоны
Скоро будет. Пока можно посмотреть в записи семинара