Семинар 2. Расстояние n-ого порядка и дифференцирование интеграла по порядку.
Содержание
Материалы
Видеозаписи
Запись семинара: youtube (16.09.23)
Расстояние между функциями n-ого порядка
Предыстория про норму
Определение. Функция \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) называется нормой, если
- \( f(x) \geq 0 \quad \forall x \in \mathbb{R}^n \) [неотрицательность]
- \( f(x) = 0 \Leftrightarrow x = 0 \)
- \( f(tx) = |t|f(x) \quad \forall x \in \mathbb{R}^n, t \in \mathbb{R} \) [гомогенность]
- \( f(x + y) \leq f(x) + f(y) \quad \forall x,y \in \mathbb{R}^n \) [неравенство треугольника]
Будем использовать обозначение \(f(x) = ||x||\) (либо \(||\cdot||_{symb}\), о чем речь пойдет ниже) для нормы (к слову, оно отсылает нас к мысли, что норма это обобщение абсолютного значения в \(\mathbb{R}\)).
Содержательный смысл нормы это длина вектора \(x \in \mathbb{R}^n\). Мы можем определить расстояние между векторами \(x\) и \(y\) с нормой \(||\cdot||\) следующим образом: \[ dist(x,y) = ||x-y|| \]
Определение. Множество векторов с нормой меньше, либо равной одному \[ \mathcal{B} = \{x \in \mathbb{R}^n \, | \, ||x|| \leq 1\} \] называют единичным шаром нормы \(||\cdot||\).
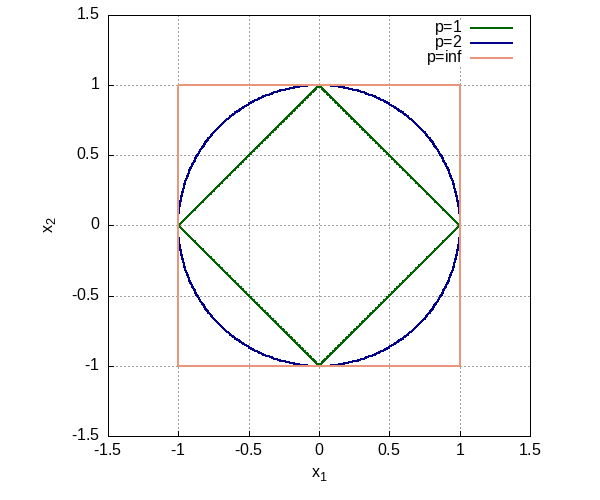
Рассмотрим примеры норм. Простой пример это \(\ell_2\) норма на \(\mathbb{R}^n\), известная по школьному курсу геометрии: \[ ||x||_2 = \sqrt{x_1^2 + x_2^2 + \ldots + x_n^2} \]
Её можно обобщить до \(\ell_p\) нормы (пространства с такой нормой обозначают \(L_p\) и иногда называют лебеговыми [в честь Анри Лебега] пространствами. В функциональном анализе это важный класс банаховых пространств) для \(p \geq 1\): \[ ||x||_p = \left( |x_1|^p + \ldots + |x_p|^p \right)^{1/p} \]
Первым краевым случаями является \(\ell_1\), которую называют taxicab или Manhattan нормой: \[ ||x||_1 = |x_1| + |x_2| + \ldots + |x_n| \]
И с другой стороны \(\ell_{\infty}\), которую называют нормой Чебышева: \[ ||x||_{\infty} = \max\{ |x_1|, \ldots, |x_n| \} \]
Для наглядности, единичные шары (точнее сферы) \(\ell_p\) норм для приведенных выше примеров изображены на рисунке ниже.
Определение расстояния n-ого порядка между функциями
Определение. расстояние n-ого порядка между двумя функциями это \[ \rho_n (y_1(t), y_2(t)) = \max_{0 \leq k \leq n} \left\{ \max_{a \leq t \leq b} \left| y_1^{(k)}(t) - y_2^{(k)}(t) \right| \right\} \]
Обратим внимание, что внутренний максимум есть ничто иное как обобщение нормы Чебышева на функциональные пространства, так как расстояние Чебышева между двумя векторами записывается как \[ dist_{\infty}(x, y) = \max_i \{ |x_i - y_i| \} \]
Но в определении выше мы дополнительно выбираем наибольшее из расстояний между функциями, между их первыми производными, вторыми производными, и так далее до производных порядка \(n\).
Задача 1
Найти расстояние между функциями при \(t \in [0, 2]\) и \( n \rightarrow \infty \): \[ y_1(t) = t^2 - 2t + 1 \] \[ y_2(t) = - t^2 + 4 \]
Решение
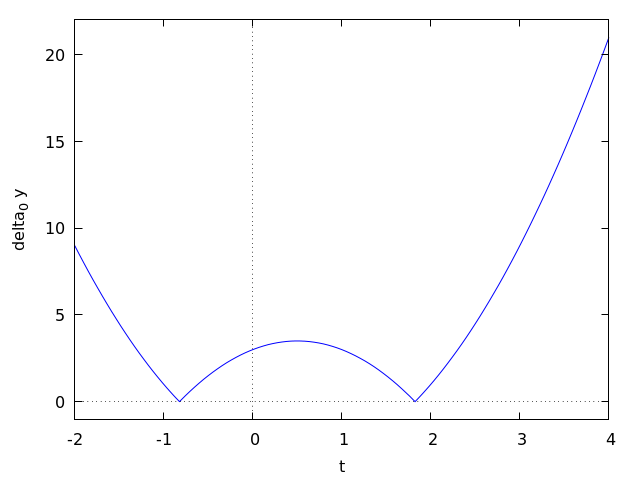
Порядок 0 \[ \delta_0y = |y_1 - y_2| = |t^2 - 2t + 1 + t^2 - 4 | = |2t^2 - 2t - 3| \]
Для максимума найдем точку экстремума внутри модуля: \( 4t - 2 = 0 \Rightarrow t^* = 1/2 \Rightarrow \delta_0y(1/2) = 3 \frac{1}{2} \)
Несмотря на то, что под модулем у нас парабола ветвями вверх, мы не можем откинуть внутренний экстремум в вершине (из-за модуля). Проверим краевые точки:
\( \delta_0 y (0) = 3, \quad \delta_0 y (2) = 1 \). Таким образом, наибольшее значение в точке \( t = 1/2 \) и, соответственно \[ \rho_0 = 3\frac{1}{2} \]
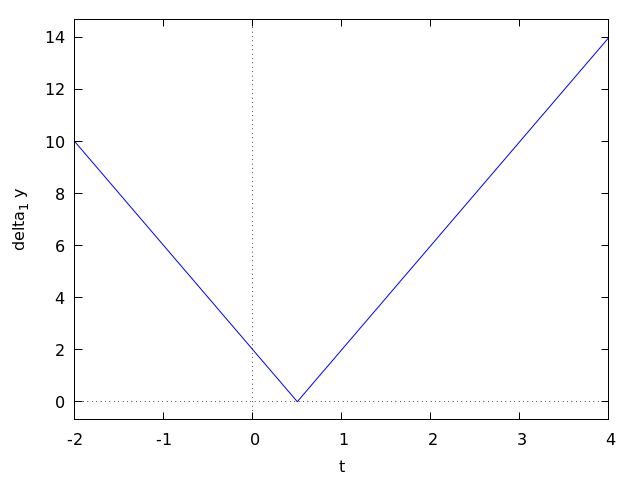
Порядок 1 \[ \delta_1 y = |y_1' - y_2'| = |4t - 2| \]
Под модулем линейная функция, которая не имеет точек экстремума. Кроме того, отметим что на интервале \(t \in [0, 2]\) модуль изламывает функцию \(4t - 2\) в точке \(t = 1/2\), но в ней \(\delta_1 y = 0\) и эта точка (к слову, точка минимума) нам не интересна, поэтому проверяем только краевые точки.
\( \delta_1 y (0) = 2, \quad \delta_1 y (2) = 6 \). Таким образом, получаем расстояние первого порядка: \[ \rho_1 = \max \left\{ 3\frac{1}{2}, 6 \right\} = 6 \]
Порядок 2+ \[ \delta_2 y = |y_1'' - y_2''| = |4|, \quad \delta_{3, 4, 5, \ldots} y = 0 \]
Во втором порядке имеем константу 4, то есть расстояние \[ \rho_2 = \max \{6, 4\} = 6 \]
Увеличивая порядок, получаем всегда 0, который очевидно меньше 6. Поэтому, при \(n \rightarrow \infty\) имеем \[ \rho_n = 6 \]
И это есть ответ в данной задаче. Ниже приведены графики для \(\delta_0y(t)\) и \(\delta_1 y(t)\) для наглядности, почему мы рассматриваем именно описанные в решении точки
Дифференцирование интеграла по параметру
Формула Лейбница
Теорема. Формула Лейбница \[ \frac{d}{d\alpha} \int_{a(\alpha)}^{b(\alpha)} f(t,\alpha) dt = \int_{a(\alpha)}^{b(\alpha)} \frac{\partial f}{\partial \alpha} dt + f(b(\alpha), \alpha) \frac{db}{d\alpha} - f(a(\alpha), \alpha) \frac{da}{d\alpha} \]
Важное напоминание: \[\frac{df}{dt}\] это полная производная, в то время как \[ \frac{\partial f}{\partial t} \] это частная производная. Пусть есть \(F(y(t), y'(t), t)\), тогда его производная по \(t\) это: \[ \frac{dF}{dt} = \frac{\partial F}{\partial t} + \frac{\partial F}{\partial y} \frac{dy}{dt} + \frac{\partial F}{\partial y'} \frac{dy'}{dt} \]
Задача 2
Дан интеграл \[ I(\alpha) = \int_0^{2\alpha} x e^{\alpha} dx \]
Найти \( \frac{d}{d\alpha} I(\alpha) \)
Решение
Подставляем аккуратно в формулу Лейбница: \[ \frac{d}{d\alpha} I(\alpha) = \int_0^{\alpha} x e^{\alpha} dx + 2 \alpha e^{\alpha} \cdot 2 - 0 \cdot 0 = \left. \frac{x^2}{2}e^{\alpha} \right|_0^{2\alpha} + 4 \alpha e^{\alpha} = \] \[ = 2\alpha^2 e^{\alpha} + 4 \alpha e^{\alpha} = (2\alpha^2 + 4\alpha) e^{\alpha} \]
В данной задаче, решение можно найти в лоб (проинтегрировать по \(x\) и взять производную по \(\alpha\)): \[ \int_0^{2\alpha} x e^{\alpha} dx = \left. \frac{x^2}{2}e^{\alpha} \right|_0^{2\alpha} = 2\alpha^2e^{\alpha} \] \[ \frac{d}{d\alpha} \left( 2\alpha^2 e^{\alpha} \right) = 4\alpha e^{\alpha} + 2\alpha^2 e^{\alpha} = (2\alpha^2 + 4\alpha) e^{\alpha}\]
Но зачастую в лоб решение не найти (см. следующую задачу).
Задача 3
Дан интеграл \[ I(\alpha) = \int_{-\alpha}^{\alpha} e^{-(x - \alpha)^2} dx \]
Найти \( \frac{d}{d\alpha} I(\alpha) \)
Решение
В отличие от предыдущей задачи, тут интеграл не берется в элементарных функциях (если посмотреть на него внимательно, то можно увидеть нечто похожее на функцию плотности нормального распределения). Используем формулу Лейбница: \[ \frac{d}{d\alpha} I(\alpha) = \int_{-\alpha}^{\alpha} 2 (x-\alpha) e^{-(x-\alpha)^2} dx + 1 \cdot 1 + e^{-4\alpha^2} = \]
Берем интеграл выше, увидев следующее: \[ = \left[ \frac{d e^{-y^2}}{dt} = -2y e^{-y^2} \right] = \left. - e^{-(x - \alpha)^2} \right|_{-\alpha}^{\alpha} + 1 + e^{-4\alpha^2} = \] \[ = -1 + e^{-4\alpha^2} + e^{-4\alpha^2} + 1 = 2 e^{-4\alpha^2} \]