Семинар 11. Условие трансверсальности. Многомерная задача оптимального управления
Содержание
Условие трансверсальности для задач оптимального управления
Небольшое напоминание лекции: для задач оптимального управления условие трансверсальности имеет вид: \[ \left[ H \right]_{t=T} \Delta T + \left[ \lambda(t) \right]_{t=T} \Delta y_T = 0 \]
То, что на прошлых семинарах мы использовали \(\lambda(T) = 0\) это как раз частный случай при фиксированном \(T\) и неизвестном \(y_T\).
Задача 1
Функция \(y(t)\) изменяется по закону \(y' = y + u\) под воздействием управления \( |u(t)| \leqslant 1 \). За это время происходит переход из состояния \(y(0) = 5\) в состояние \(y(T) = 11\). Найдите минимальное \(T\).
Решение
Сформулируем задачу как задачу оптимального управления \[ T \rightarrow \min \Leftrightarrow \int_0^T -1 \, dt \rightarrow \max \] \[ y' = y + u, \quad y(0) = 5, \quad y(T) = 11, \quad u \in [-1, 1] \]
Идем по пунктам.
1. Гамильтониан
\[ H = -1 + \lambda y + \lambda u \]
2. Максимум гамильтониана по управлению
\[ u = \begin{cases} 1, & \lambda > 0 \\ [-1,1], & \lambda = 0 \\ -1, & \lambda < 0 \\ \end{cases}\]
3. Каноническая система
Сначала решаем уравнение для \(\lambda\): \[ \lambda' = - \frac{\partial H}{\partial y} = - \lambda \] \[ \lambda = C_1 e^{- t} \]
Из условия трансверсальности (пункт 4): \[ H_{t=T} = 0 \Rightarrow -1 + C_1 e^{-T} (11 + u) = 0 \Rightarrow C_1 = \frac{e^{T}}{11 + u} > 0 \,\, (u \in [-1, 1]) \] Так как \(C_1 > 0\), то и на интервале \(t \in [0, T]\) для любого \(T\) будет \(\lambda > 0\), и тогда \(u = 1\).
Видим, что на интервале \(t \in [0, 2]\) значение \(\lambda \geqslant 0\), а значит \(u(t) = 1\).
Переходим ко второму уравнению (для \(y\)): \[ y' = y + u = y + 1 \] \[ y = C_2 e^{t} - 1 \]
Из граничного условия найдем константу: \[ y(0) = 5 \Rightarrow C_2 = 6 \] \[ y(t) = 6e^t - 1 \]
Из второго граничного условия получим значение \(T\): \[ \]\[ y(T) = 11 \Rightarrow 6e^T - 1 = 11 \Rightarrow T = \ln 2 \]
Ответ:
Траектория \[ y(t) = 6e^{t} - 1 \] доставляет максимум функционалу при управлении \[u(t) = 1\] и \(T = \ln 2\)
Задача многомерного оптимального управления
Постановка задачи
Задача имеет следующий вид: \[ \int_0^T F(y,u,t) \, dt \rightarrow \max \] \[ y' = f(y,u,t), \quad y(0) = y_0, \quad u \in U \] \[ y = (y_1, \ldots, y_n), \, u = (u_1, \ldots, u_m), \, f = (f_1, \ldots, f_n)\]
Принцип максимума
Для решения многомерной задачи оптимального управления следующие шаги (аналогично принципу максимума Понтрягина для одномерной задачи):
- Выписываем Гамильтониан: \[ H = F + \sum_{i=1}^{n} \lambda_i f_i \]
- Гамильтониан достигает максимума для каждого \(u\): \[ \max_{u \in U} H \]
- Каноническая система: \[ \land_{i=\overline{1, n}} \quad y_i' = \frac{\partial H}{\partial \lambda_i}, \,\, \lambda_i' = - \frac{\partial H}{\partial y_i} \]
- Условие трансверсальности: \[ \left[ H \right]_{t=T} \Delta T - \sum_{i=1}^n \lambda_i(T) \Delta y_{i T} = 0 \]
Задача 2
Рассмотрим движение материальной точки единичной массы под действием управления. В начальном состоянии \(y(0) = y_0\), а конечное: \(y(T) = 0\). Такой переход должен произойти на наименьшее \(T\) и с конечной нулевой скоростью. Про скорость известно следующее: \[ z(0) = z_0, \, z(T) = 0 \] Также известно уравнение движения: \[ y'' = u \quad (ma = F), \quad u \in [-1, 1] \]
Решение
Интуиция: релейное переключение (сначала ускоряемся, потом тормозим, чтобы остановиться в нужной точке).
Перепишем задачу в стандартном виде: \[ \int_0^T -1 \, dt \rightarrow \max \] \[ \]\[ y' = z, \, z' = u \] \[ y(0) = y_0, \, z(0) = z_0, \, y(T) = 0, z(T) = 0 \] \[ u \in [-1, 1] \]
Идем по пунктам.
-
Выписываем Гамильтониан: \[ H = -1 + \lambda_y z + \lambda_z u \]
-
Максимум Гамильтониана по управлению: \[ u = \begin{cases} 1, & \lambda_z > 0 \\ [-1,1], & \lambda_z = 0 \\ -1, & \lambda_z < 0 \\ \end{cases} \]
-
Каноническая система: \[ \lambda_y' = - \frac{\partial H}{\partial y} = 0 \Rightarrow \lambda_y = C_1 \] \[ \lambda_z' = - \frac{\partial H}{\partial z} = - \lambda_y \Rightarrow \lambda_z' = -C_1 \] \[\lambda_z = -C_1 t + C_2\]
Из линейности \(\lambda_z\) можем сделать вывод, что переключений не более одного. Рассмотрим четыре возможных случая.
-
Случай \(u = 1\) (тормозим при начальной отрицательной скорости) \[ z' = 1 \Rightarrow z = t + C_3 \] \[ y' = z \Rightarrow y = \frac{t^2}{2} + C_3 t + C_4 \]
Из начальных условий: \(C_3 = z_0, \, C_4 = y_0\)
Из уравнения для \(z\) можем выразить \(t\) и подставить в уравнение для \(y\): \[ t = z - z_0 \Rightarrow y = \frac{(z - z_0)^2}{2} + z_0 (z - z_0) + y_0 \] \[ y = \frac{z^2}{2} - z \cdot z_0 + \frac{z_0^2}{2} + z \cdot z_0 + y_0 = \frac{z^2}{2} + \varphi(z_0, y_0) \]
Нарисуем фазовое пространство (\(z\) со временем растет):
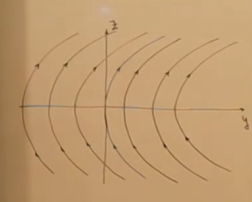
Figure 1: Фазовое пространство Случай один возможен, только если \(z_0, y_0\) лежат на траектории, проходящей через (0,0) и только в четвертом квадранте.
-
Случай \(u = -1\) (тормозим положительную скорость) \[ z = -t + C_5 \] \[ y = -\frac{t^2}{2} + C_5 t + C_6 \]
Фазовое пространство аналогично прошлому пункту, только теперь парабола \(-z^2/2\) и \(z\) со временем падает, а не растёт. Поэтому случай возможен, только если \(z_0, y_0\) лежат на траектории, проходящей через (0,0) и только во втором квадранте.
-
Случаи с переключением
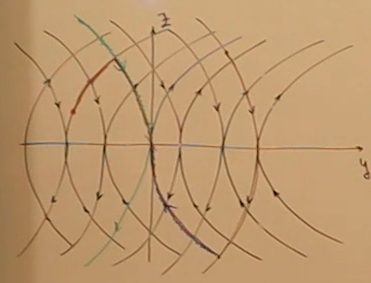
Figure 2: Фазовое пространство Из любой точки идем либо до траектории из первого случая, либо до траектории из второго. По графику можно понять в каком порядке следуют режимы.
Рассмотрим случай, когда \(u = 1\) при \(t \in [0, \tau)\) и \(u = -1\) при \(t \in [\tau, T]\).
При \(t \in [0, \tau)\): \[z = t + z_0\] \[y = \frac{t^2}{2} + z_0 y + y_0 \]
При \(t \in [\tau, T]\): \[z = -t + C_5\] \[ y = - \frac{t^2}{2} + C_5 t + C_6 \]
Можем найти константы из конечных условий: \[ z(T) = 0 \Rightarrow C_5 = T \] \[ y(T) = 0 \Rightarrow C_6 = -\frac{T^2}{2} \]
Условие трансверсальности в данном случае имеет вид: \[ \left[ H \right]_{t = T} = 0 \Rightarrow -1 + \lambda_y(T) z(T) + \lambda_z(T) u = 0 \] В исследуемом нами случае: \[ -1 - (-C_1 T + C_2) = 0 \] Проблема в том, что отсюда мы можем найти только константы для уравнений для двойственной переменной (использовав ещё факт, что в точке переключения \(\lambda_z = 0\)), которые нам не нужны.
Для того, чтобы найти \(T\) и \(\tau\) нам хватит просто факта непрерывности \(z(t)\) и \(y(t)\).
-